Question
There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:
- There are no self-edges (
graph[u]does not containu). - There are no parallel edges (
graph[u]does not contain duplicate values). - If
vis ingraph[u], thenuis ingraph[v](the graph is undirected). - The graph may not be connected, meaning there may be two nodes
uandvsuch that there is no path between them.
A graph is bipartite if the nodes can be partitioned into two independent sets Aand B such that every edge in the graph connects a node in set A and a node in set B.
Return true iff, it is bipartite.
Example 1:
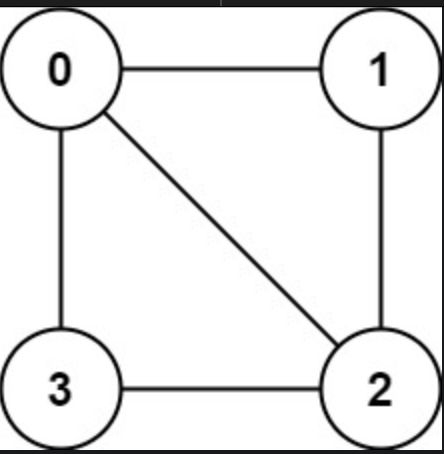
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]] Output: false Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
Example 2:
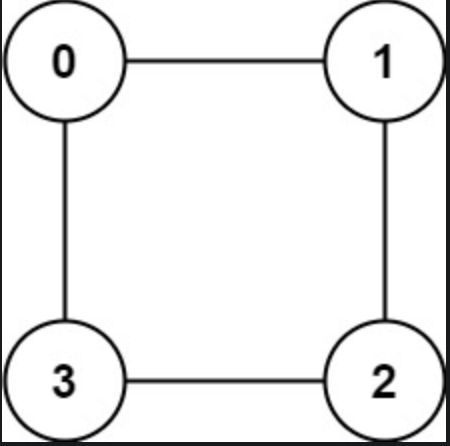
Input: graph = [[1,3],[0,2],[1,3],[0,2]] Output: true Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
BFS Solution:
class Solution {
class NodeLevel {
int node;
int level;
NodeLevel(int node, int level) {
this.node = node;
this.level = level;
}
}
public boolean isBipartite(int[][] graph) {
boolean[] visited = new boolean[graph.length];
int[] nodeLevels = new int[graph.length];
Arrays.fill(nodeLevels, -1); // Initialize nodeLevels to -1, indicating unvisited nodes
// Iterate over all nodes to handle disconnected components
for (int i = 0; i < graph.length; i++) {
if (!visited[i]) {
// If the component starting at node i is not bipartite, return false
if (!bfsCheckBipartite(graph, visited, i, nodeLevels)) {
return false;
}
}
}
return true; // All components are bipartite
}
public boolean bfsCheckBipartite(int[][] graph, boolean[] visited, int startNode, int[] nodeLevels){
// BFS initialization
ArrayDeque<NodeLevel> q = new ArrayDeque<>();
q.add(new NodeLevel(startNode, 0));
while(q.size() > 0){
NodeLevel current = q.removeFirst();//remove
//mark*
if(visited[current.node]){
if(current.level != nodeLevels[current.node]){
return false;
}
} else{
visited[current.node] = true;
nodeLevels[current.node] = current.level;
}
//work - No work
//add*
for(int neighbor: graph[current.node]){
if(!visited[neighbor]){
q.add(new NodeLevel(neighbor, current.level + 1));
}
}
}
return true; // No conflicts found, component is bipartite
}
}Dry Run

DFS Solution:
Our goal is trying to use two colors to color the graph and see if there are any adjacent nodes having the same color.
Initialize a color[] array for each node. Here are three states for colors[] array:
0: Haven't been colored yet.
1: Blue.
-1: Red.
For each node,
- If it hasn’t been colored, use a color to color it. Then use the other color to color all its adjacent nodes (DFS).
- If it has been colored, check if the current color is the same as the color that is going to be used to color it
class Solution {
public boolean isBipartite(int[][] graph) {
int n = graph.length;
int[] colors = new int[n];
//This graph might be a disconnected graph. So check each unvisited node.
for (int i = 0; i < n; i++) {
if (colors[i] == 0 && !validColor(graph, colors, 1, i)) {
return false;
}
}
return true;
}
public boolean validColor(int[][] graph, int[] colors, int color, int node) {
if (colors[node] != 0) {
return colors[node] == color;
}
colors[node] = color;
for (int next : graph[node]) {
if (!validColor(graph, colors, -color, next)) {
return false;
}
}
return true;
}
}