Kth Smallest Number in Multiplication Table

Problem Statement:

Nearly everyone has used the Multiplication Table. The multiplication table of size m x n is an integer matrix matwhere mat[i][j] == i * j (1-indexed). Given three integers m, n, and k, return the kth smallest element in the m x n multiplication table.

Example 1:

Open: Screenshot 2024-06-19 at 5.15.23 PM.png

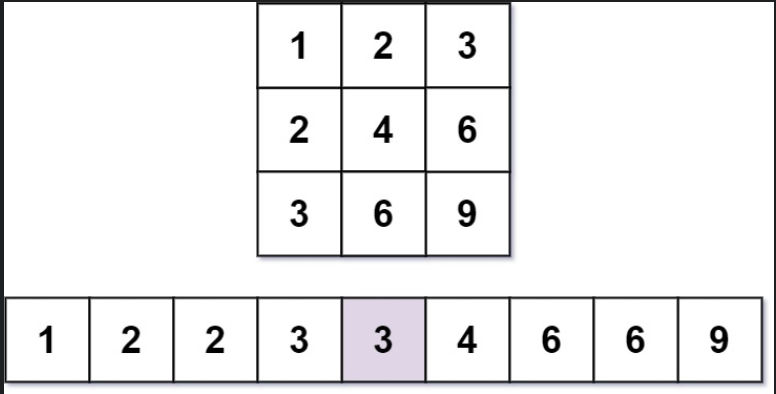
Input: m = 3, n = 3, k = 5 Output: 3 Explanation: The 5th smallest number is 3.

Example 2:

Open: Screenshot 2024-06-19 at 5.15.50 PM.png

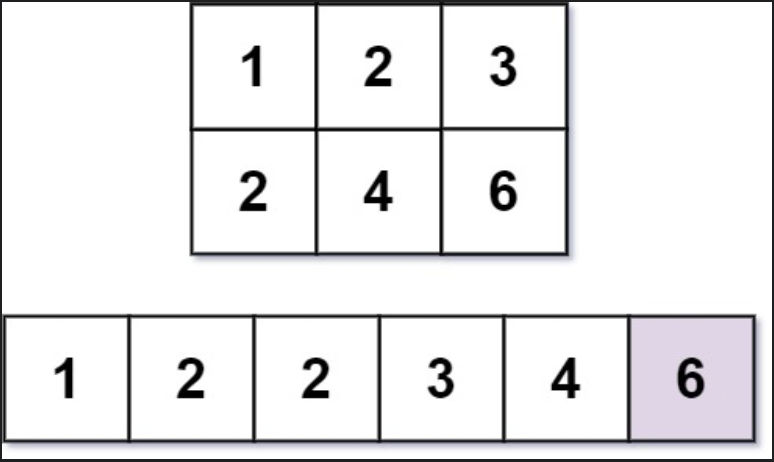
Input: m = 2, n = 3, k = 6 Output: 6 Explanation: The 6th smallest number is 6.

Constraints:

• 1 <= m, n <= 3 * 10^4
• 1 <= k <= m * n

Solution:

class Solution {
    private boolean hasAtLeastKSmallerNumbers(int m, int n, int k, int num) {
        int count = 0; // Counter for the numbers less than or equal to 'num'.
        
        // Iterate over each row to count how many numbers in the multiplication table are <= 'num'.
        for (int row = 1; row <= m; row++) {
            /*  Count the numbers in this row that are <= 'num'.
                (num / row) gives the highest column index with value <= 'num' for the current row.
                We take the minimum with 'n' to handle cases where num / row > n.
            */
            count += Math.min(num / row, n);
        }
        
        // Check if we have counted at least 'k' numbers.
        return count >= k;
    }
 
    public int findKthSmallestNumber(int m, int n, int k) {
        //Define the search space
        int left = 1; // Minimum possible value in the table.
        int right = m * n; // Maximum possible value in the table.
 
        // Perform binary search to find the k-th smallest number.
        while (left < right) {
            int mid = left + (right - left) / 2;
            
            // Check if 'mid' can be the k-th smallest number.
            if (hasAtLeastKSmallerNumbers(m, n, k, mid)) {
                right = mid; // If yes, look for smaller values.
            } else {
                left = mid + 1; // Otherwise, look for larger values.
            }
        }
        
        // The left boundary now points to the k-th smallest number.
        return left;
    }
}