Symmetric Trees

Problem Statement:

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

Example 1:

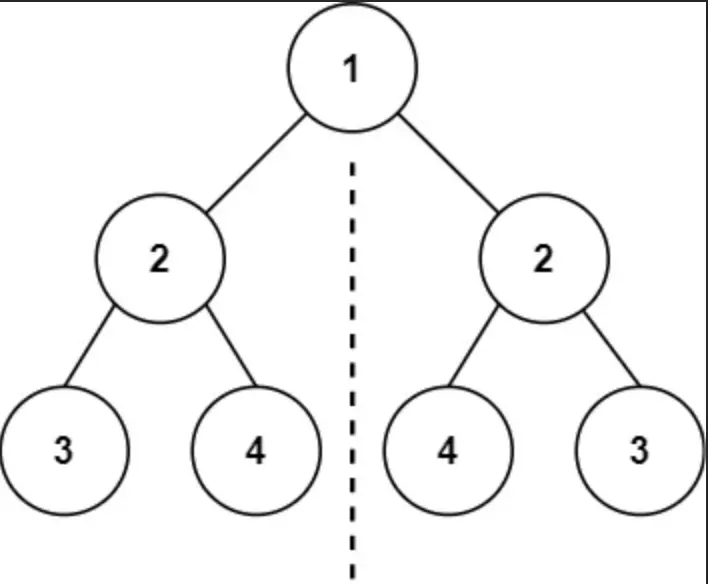
Input: root = [1,2,2,3,4,4,3] Output: true

Example 2:

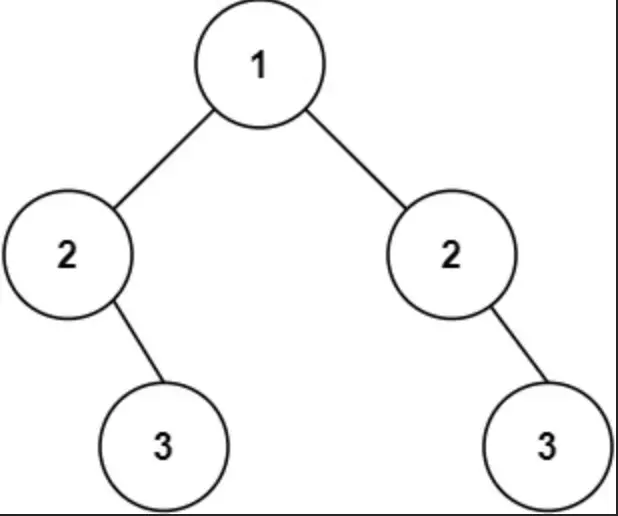
Input: root = [1,2,2,null,3,null,3] Output: false

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• -100 <= Node.val <= 100

Solution:

1. Recursive:

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return isSymmetric_(root, root);
    }
 
    public boolean isSymmetric_(TreeNode leftT, TreeNode rightT) {
        if(leftT == null && rightT == null){
            return true;
        }
        if(leftT == null || rightT == null){
            return false;
        }
 
        return leftT.val == rightT.val && 
        isSymmetric_(leftT.left, rightT.right) && 
        isSymmetric_(leftT.right, rightT.left);
    }
}

2. Iterative Approach

class Solution {
    public boolean isSymmetric(TreeNode root) {
        LinkedList<TreeNode> q = new LinkedList<>();
        q.add(root);
        q.add(root);
        
        while(!q.isEmpty()){
            TreeNode r1 = q.poll();
            TreeNode r2 = q.poll();
            
            if(r1 == null && r2 == null)
                continue;
            if(r1 == null || r2 == null)
                return false;
                
            
            if(r1.val == r2.val){
                q.add(r1.left);
                q.add(r2.right);
                
                q.add(r1.right);
                q.add(r2.left);
            }
            else
                return false;
            
            
        }
        return true;
    }
}