Unique Paths

Question:

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time. Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

Example 1:

Open: Screenshot 2024-06-14 at 8.52.31 PM.png

Input: m = 3, n = 7 Output: 28

Example 2:

Input: m = 3, n = 2 Output: 3 Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:

1. Right → Down → Down
2. Down → Down → Right
3. Down → Right → Down

Solution:

Memoized approach

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] memo = new int[m][n];
        for(int[] arr: memo){
            Arrays.fill(arr, -1);
        }
 
        // memo[m-1][n-1] = 0;
        return uniquePathsHelper(0, 0, m - 1, n - 1, memo);
    }
 
    public int uniquePathsHelper(int sr, int sc, int dr, int dc, int[][] memo){
        if(sr > dr || sc > dc){
            return 0;
        }
        if(sr == dr && sc == dc){
            return 1;
        }
 
        if(memo[sr][sc] != -1){
            return memo[sr][sc];
        }
 
        int right = uniquePathsHelper(sr, sc + 1, dr, dc, memo);
        int down = uniquePathsHelper(sr + 1, sc, dr, dc, memo);
 
        return memo[sr][sc] = down + right;
    }
}

Tabulation approach:

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        //There is only one way to reach destination from destination
        dp[m - 1][n - 1] = 1;
        
        // Fill the last row
        for (int j = n - 2; j >= 0; j--) {
            dp[m - 1][j] = 1;
        }
        
        // Fill the last column
        for (int i = m - 2; i >= 0; i--) {
            dp[i][n - 1] = 1;
        }
	    
        for(int i = m - 2; i >= 0; i--){
            for(int j = n - 2; j >= 0; j--){
                dp[i][j] = dp[i + 1][j] + dp[i][j + 1];
            }
        }
 
        return dp[0][0];
    }
}

Space optimization:

To calculate the final result we only need prev row and curr row’s next element.

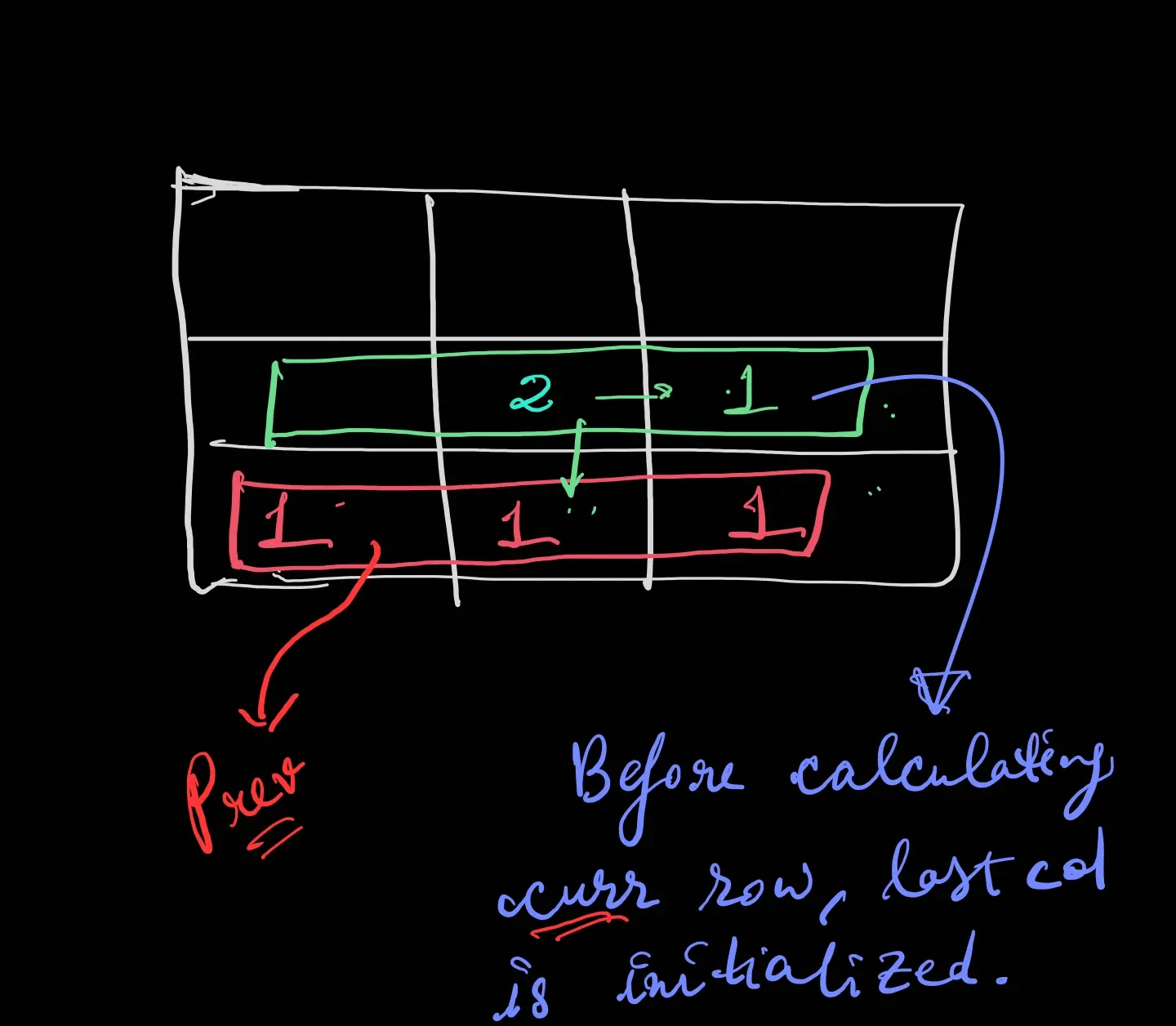
class Solution {
    public int uniquePaths(int m, int n) {
        int[] prev = new int[n];
 
		Arrays.fill(prev, 1); // Initialize the last row with 1s since there's only one way to reach the destination
		
		// Fill the grid from bottom to top
		for(int i = m - 2; i >= 0; i--){
			
			int[] curr = new int[n];
			curr[n - 1] = 1; // Initialize the last column for the current row (only one way to reach the destination by moving down)
			
			// Update the current row based on the values from the previous row
			for(int j = n - 2; j >= 0; j--){
				curr[j] = curr[j + 1] + prev[j]; // Sum of ways from the cell to the right and the cell directly below
			}
			
			prev = curr;
		}
		return prev[0];
    }
}