Problem statement:
Given two strings str1 and str2, return the shortest string that has both str1and str2 as subsequences. If there are multiple valid strings, return any of them.
A string s is a subsequence of string t if deleting some number of characters from t (possibly 0) results in the string s.
Example 1: Input: str1 = “abac”, str2 = “cab” Output: “cabac” Explanation: str1 = “abac” is a subsequence of “cabac” because we can delete the first “c”. str2 = “cab” is a subsequence of “cabac” because we can delete the last “ac”. The answer provided is the shortest such string that satisfies these properties.
Solution:
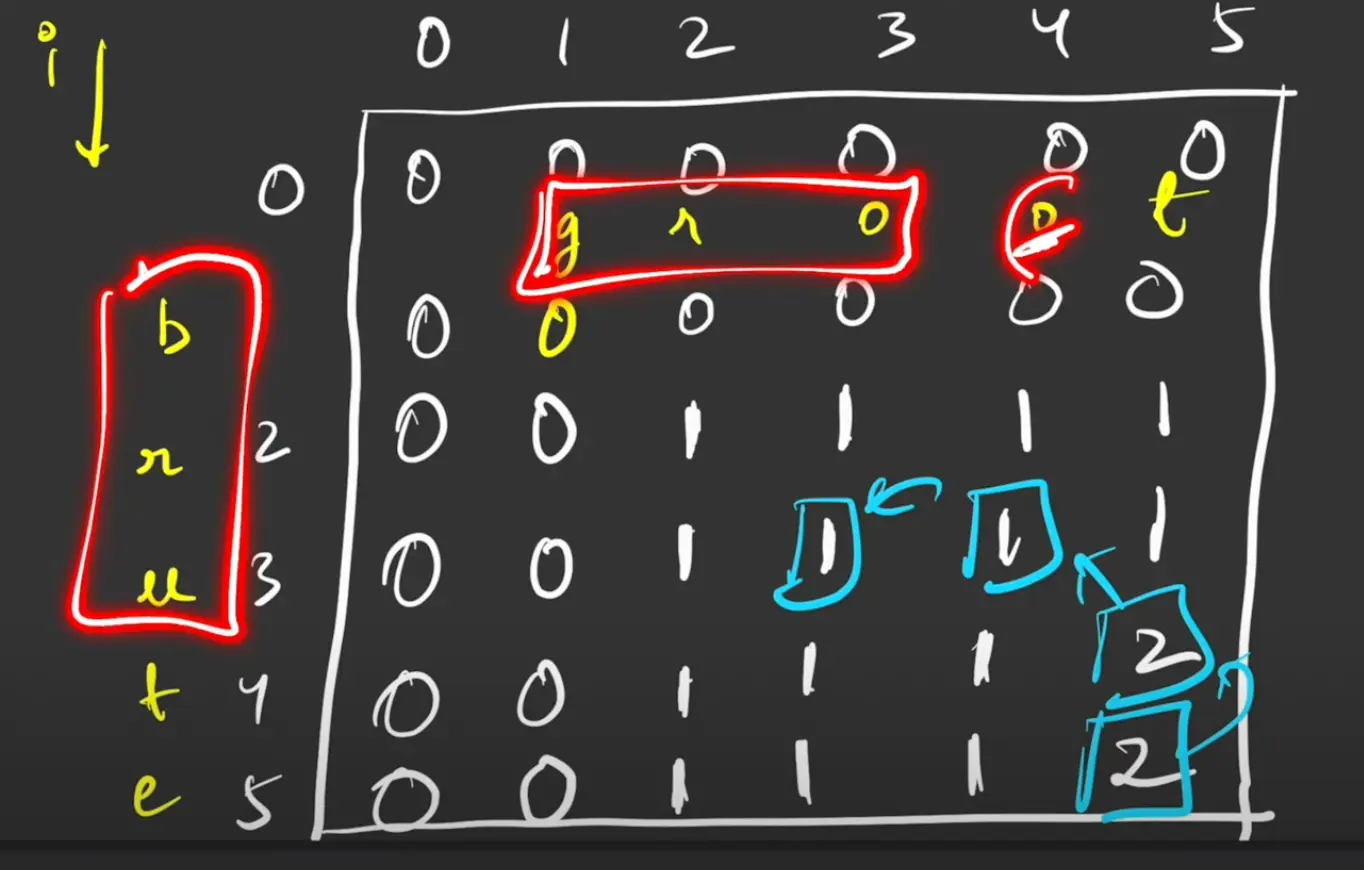
- Calculate the dp table (same as Tabulation ) and We’ll make our answer from dp[n1][n2] and trace back till one of the row or column reaches it’s limit.
class Solution {
public String shortestCommonSupersequence(String str1, String str2) {
int n1 = str1.length();
int n2 = str2.length();
int[][] dp = new int[n1 + 1][n2 + 1];
// Fill the DP table to find the length of LCS
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
// Characters match, add 1 to the result from the previous indices
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
// Characters don't match, take the maximum of ignoring one character from either string
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// Reconstruct the Shortest Common Supersequence from the DP table
int i = n1;
int j = n2;
StringBuilder sb = new StringBuilder();
// Trace back through the DP table to build the SCS
while (i > 0 && j > 0) {
char ch1 = str1.charAt(i - 1);
char ch2 = str2.charAt(j - 1);
if (ch1 == ch2) {
// If characters match, it is part of the LCS
sb.append(ch1);
i--;
j--;
} else if (dp[i - 1][j] >= dp[i][j - 1]) {
// If characters don't match, choose the direction with the larger value in the DP table
// This helps to keep the maximum length of LCS
sb.append(ch1);
i--;
} else {
sb.append(ch2);
j--;
}
}
// Append any remaining characters from str1
while (i > 0) {
sb.append(str1.charAt(i - 1));
i--;
}
// Append any remaining characters from str2
while (j > 0) {
sb.append(str2.charAt(j - 1));
j--;
}
// The built string is in reverse order, reverse it to get the correct order
return sb.reverse().toString();
}
}