Minimum Height Trees

Question:

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree. Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h))  are called minimum height trees (MHTs).

Return a list of all MHTs’ root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

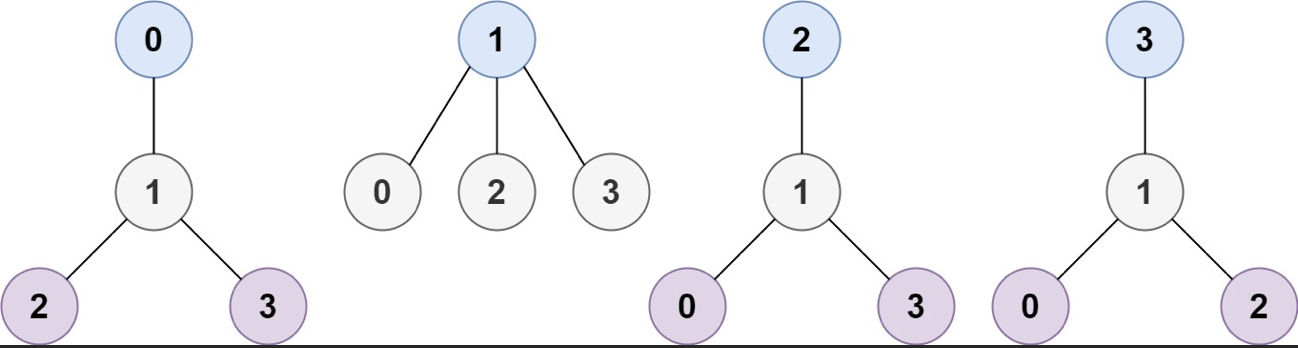
Input: n = 4, edges = [[1,0],[1,2],[1,3]] Output: [1] Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

Open: Screenshot 2024-06-21 at 4.38.40 PM.png

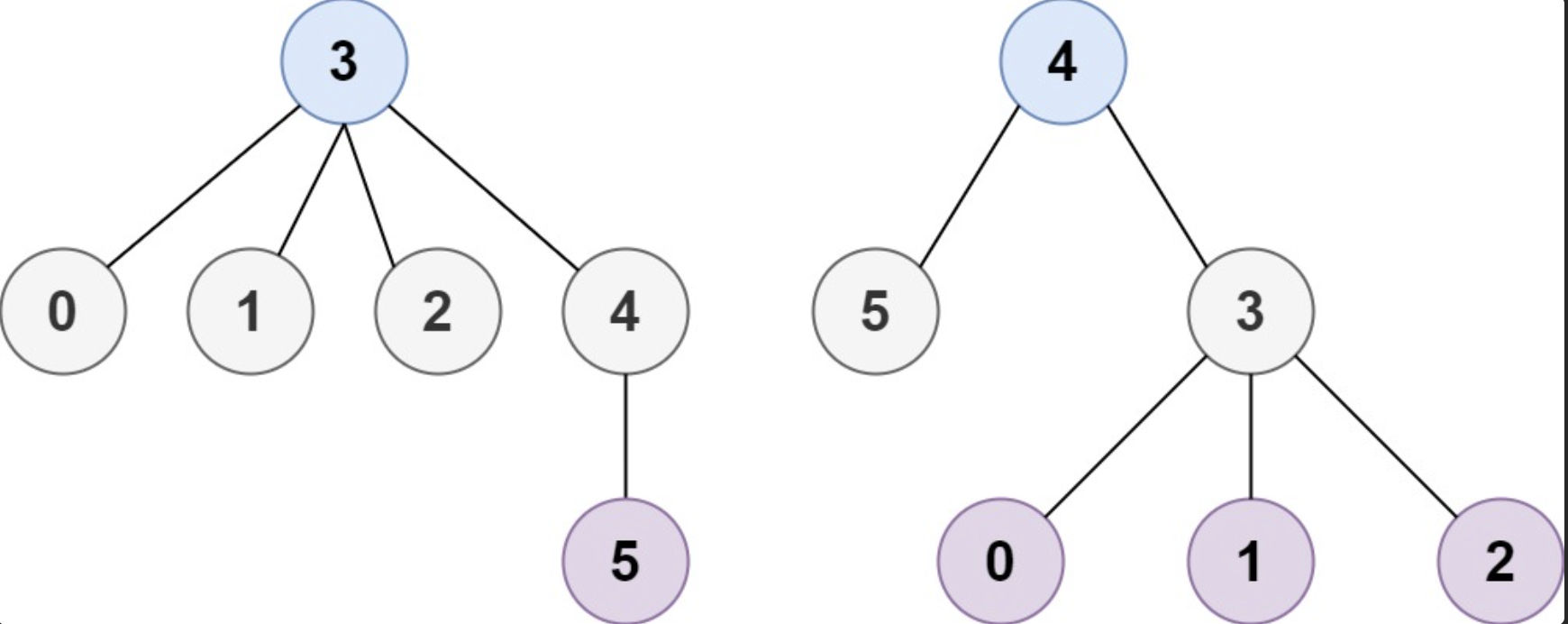
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]] Output: [3,4]

Solution:

1. Brute Force: (Ran BFS for every node while maintaining a array which contains min distance for each node)

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        List<Integer> minDistList = new ArrayList<>();
        
        ArrayList<Integer>[] graph = new ArrayList[n];
        for(int i = 0; i < n; i++){
            graph[i] = new ArrayList<>();
        }
        for(int[] edge: edges){
            int u = edge[0];
            int v = edge[1];
            graph[u].add(v);
            graph[v].add(u);
        }
 
        for(int i = 0; i < n; i++){
            int minDist = Integer.MIN_VALUE;
            Queue<int[]> q = new LinkedList<>();
            boolean[] vis = new boolean[n];
            q.offer(new int[]{i, 0});
 
            while(!q.isEmpty()){
                int[] curr = q.remove();
                int currV = curr[0];
                int dist = curr[1];
 
                if(vis[currV] == true) continue;
                vis[currV] = true;
 
                minDist = Math.max(minDist, dist);
 
                for(int edge: graph[currV]){
                    if(!vis[edge]){
                        q.offer(new int[]{edge, dist + 1});
                    }
                }
            }
            minDistList.add(minDist);
        }
        int minVal = Integer.MAX_VALUE;
        for(int i = 0; i < minDistList.size(); i++){
            minVal = Math.min(minVal, minDistList.get(i));
        }
 
        List<Integer> ans = new ArrayList<>();
        for(int i = 0; i < minDistList.size(); i++){
            if(minDistList.get(i) == minVal){
                ans.add(i);
            }
        }
 
        return ans;
    }
}

2. Optimized solution

Observations and Intuition:

1. In a tree, the minimum height is achieved when the root is chosen such that the heights of its subtrees are as balanced as possible.
2. The nodes that can be the roots of MHTs are the centroids of the tree.
3. The centroids of a tree are the nodes that minimize the maximum distance to any other node in the tree.
4. In a tree, there can be at most two centroids.
5. We can iteratively remove the leaves (nodes with only one neighbor) until we are left with one or two nodes, which will be the centroids.

Optimized Approach (Topological Sorting):

1. Create an adjacency list to represent the tree.

2. Initialize a list to store the degrees of each node (number of neighbors).

3. Initialize a queue to perform a topological sorting-like process.

4. Enqueue all the leaves (nodes with only one neighbor) into the queue.

5. While the number of remaining nodes is greater than 2:

6. Dequeue a node from the queue.

7. Decrement the degree of its neighbor.

8. If the neighbor becomes a leaf (degree becomes 1), enqueue it.

9. The remaining one or two nodes in the queue are the roots of the MHTs. Time complexity: O(n), where n is the number of nodes. Space complexity: O(n) to store the adjacency list and the queue.

public class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        // Special case for a single node
        if (n == 1) {
            return Collections.singletonList(0);
        }
 
        // Initialize the graph as an array of ArrayLists
        List<Integer>[] graph = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        
        // Initialize the in-degrees array
        int[] inDegrees = new int[n];
        
        // Build the graph and populate in-degrees
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];
            graph[u].add(v);
            graph[v].add(u);
            inDegrees[u]++;
            inDegrees[v]++;
        }
        
        // Initialize the queue with leaf nodes
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < n; i++) {
            if (inDegrees[i] == 1) {
                queue.offer(i);
            }
        }
        
        // Perform BFS to remove leaves layer by layer
        List<Integer> remainingNodes = new ArrayList<>();
        while (!queue.isEmpty()) {
            remainingNodes = new ArrayList<>(); // Nodes remaining after the current layer is removed
            int size = queue.size();
            
            for (int i = 0; i < size; i++) {
                int leaf = queue.poll();
                remainingNodes.add(leaf);
                for (int neighbor : graph[leaf]) {
                    inDegrees[neighbor]--;
                    if (inDegrees[neighbor] == 1) { // If it becomes a leaf, add to queue
                        queue.offer(neighbor);
                    }
                }
            }
        }
        
        // Remaining nodes are the roots of the MHTs
        return remainingNodes;
    }
}