- It’s same as BFS, but Queue is replaced by PriorityQueue!
- Where to use?:
- Find the shortest path from a single source vertex to all other vertices in a weighted graph.
- Calculates the minimum distance (or cost) to reach each vertex from the source vertex.
Dijkstra Negative Cycle Issue!
⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠
Text Elements
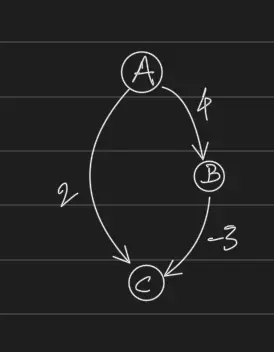
V={A,B,C} ; E = {(A,C,2), (A,B,5), (B,C,-10)}
A
B
C
5
2
-10
Dijkstra from A will first develop C, and will later fail to find A→B→C
Link to original
1st Version of Dijkstra’s version (Recommended)
- BFS Analogy:
- Breadth-First Search (BFS) is an algorithm used to explore the shortest paths in an unweighted graph. BFS processes nodes level by level, ensuring that the shortest path to each node (in terms of the number of edges) is found before moving on to nodes further away.
- In a weighted graph, where edges have different costs, the concept of “distance” becomes more complex. Dijkstra’s algorithm extends the idea of BFS by using a priority queue to manage which node to process next, based on the shortest known distance rather than the number of edges.
- How It Works:
- Both BFS and Dijkstra start from a source node and explore its neighbors.
- In BFS, all neighbors are added to the queue with equal priority.
- In Dijkstra, neighbors are added to the priority queue, and their priority is determined by the shortest known distance from the source. The priority queue ensures that the node with the smallest distance is processed next, which might not follow the strict level-by-level processing of BFS.
import java.util.*;
public class Main {
static class Edge {
int src;
int dest;
int weight;
Edge(int src, int dest, int weight) {
this.src = src;
this.dest = dest;
this.weight = weight;
}
}
static class PathNode implements Comparable<PathNode> {
int node;
String pathSoFar;
int weightSoFar;
PathNode(int node, String pathSoFar, int weightSoFar) {
this.node = node;
this.pathSoFar = pathSoFar;
this.weightSoFar = weightSoFar;
}
public int compareTo(PathNode other) {
return this.weightSoFar - other.weightSoFar;
}
}
// Dijkstra's algorithm implementation
private static void dijkstra(ArrayList<Edge>[] graph, int source) {
PriorityQueue<PathNode> priorityQueue = new PriorityQueue<>();
boolean[] visited = new boolean[graph.length];
priorityQueue.add(new PathNode(source, source + "", 0));
while (!priorityQueue.isEmpty()) {
PathNode currentPair = priorityQueue.remove();
// Skip processing if the node is already visited
if (visited[currentPair.node]) {
continue;
}
// Mark the node as visited
visited[currentPair.node] = true;
// Output the shortest path to the current node
System.out.println(currentPair.node + " via " + currentPair.pathSoFar + " weight: " + currentPair.weightSoFar);
// Explore the neighbors of the current node
for (Edge edge : graph[currentPair.node]) {
if (!visited[edge.dest]) {
priorityQueue.add(new PathNode(edge.dest, currentPair.pathSoFar + " -> " + edge.dest, currentPair.weightSoFar + edge.weight));
}
}
}
}
public static void main(String[] args) {
// Example usage:
int vertices = 5;
ArrayList<Edge>[] graph = new ArrayList[vertices];
for (int i = 0; i < vertices; i++) {
graph[i] = new ArrayList<>();
}
// Adding edges
graph[0].add(new Edge(0, 1, 4));
graph[0].add(new Edge(0, 2, 1));
graph[2].add(new Edge(2, 1, 2));
graph[1].add(new Edge(1, 3, 1));
graph[2].add(new Edge(2, 3, 5));
graph[3].add(new Edge(3, 4, 3));
// Running Dijkstra's algorithm from source node 0
dijkstra(graph, 0);
}
}
//==== output =====
0 via 0 weight: 0
2 via 0 -> 2 weight: 1
1 via 0 -> 2 -> 1 weight: 3
3 via 0 -> 2 -> 1 -> 3 weight: 4
4 via 0 -> 2 -> 1 -> 3 -> 4 weight: 7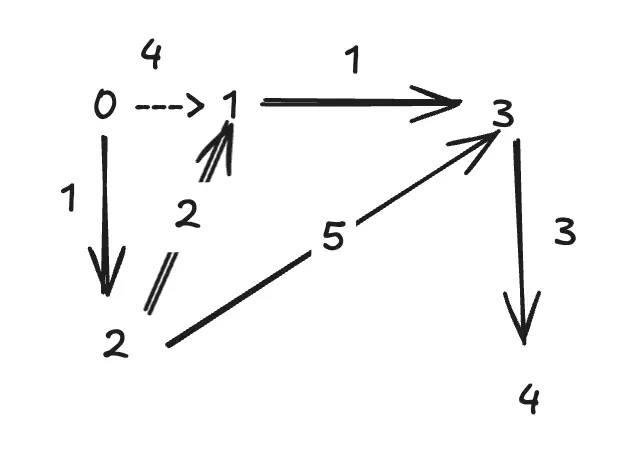
2nd version of Dijkstra’s algorithm
Dijkstra as an Edge Relaxation Algorithm
- Edge Relaxation:
- The edge relaxation perspective focuses on how Dijkstra’s algorithm repeatedly attempts to “relax” edges by finding shorter paths to each vertex through its neighbors.
- This view emphasizes the iterative improvement of shortest path estimates until the algorithm converges on the final shortest paths.
- Steps of Relaxation:
- In each iteration, the algorithm picks the vertex with the smallest known distance (using the priority queue), processes it, and tries to update (relax) the distances to its neighbors based on the current shortest path.
Dijkstra’s Algorithm in Terms of Edge Relaxation
- Initialization:
- Start with the source vertex, setting its distance to 0 (dist[source] = 0) and all other vertices to infinity (dist[v] = ∞ for all other vertices v).
- Use a priority queue to manage the vertices, initially containing only the source vertex.
- Relaxation Process:
- While the priority queue is not empty, do the following:
- Extract the vertex u with the smallest known distance (dist[u]) from the priority queue.
- For each neighboring vertex v connected to u by an edge (u, v) with weight w, attempt to relax the edge:
- If
dist[v] > dist[u] + w, then updatedist[v] = dist[u] + w. - Add or update vertex v in the priority queue with the new distance dist[v].
- Repeat:
- Continue this process until all vertices have been processed (i.e., the priority queue is empty).
import java.util.*;
class Node implements Comparable<Node> {
int vertex;
int weight;
Node(int vertex, int weight) {
this.vertex = vertex;
this.weight = weight;
}
@Override
public int compareTo(Node other) {
return this.weight - other.weight;
}
}
public class Dijkstra {
private static void dijkstra(int[][] graph, int source) {
int V = graph.length;
int[] dist = new int[V];
boolean[] visited = new boolean[V];
PriorityQueue<Node> pq = new PriorityQueue<>();
// Initialize distances to infinity and visited to false
Arrays.fill(dist, Integer.MAX_VALUE);
dist[source] = 0;
// Start with the source node
pq.add(new Node(source, 0));
while (!pq.isEmpty()) {
// Extract the node with the minimum distance
Node current = pq.poll();
int u = current.vertex;
if (visited[u]) continue;
visited[u] = true;
// Process all adjacent vertices of the extracted node
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && !visited[v] && dist[u] != Integer.MAX_VALUE) {
int newDist = dist[u] + graph[u][v];
if (newDist < dist[v]) {
dist[v] = newDist;
pq.add(new Node(v, dist[v]));
}
}
}
}
// Print the shortest distances
System.out.println("Vertex \t\t Distance from Source");
for (int i = 0; i < V; i++) {
System.out.println(i + " \t\t " + dist[i]);
}
}
public static void main(String[] args) {
int[][] graph = {
{ 0, 10, 0, 0, 0, 0 },
{ 10, 0, 5, 0, 0, 0 },
{ 0, 5, 0, 15, 0, 0 },
{ 0, 0, 15, 0, 10, 5 },
{ 0, 0, 0, 10, 0, 20 },
{ 0, 0, 0, 5, 20, 0 }
};
int source = 0;
dijkstra(graph, source);
}
}Key Points in Edge Relaxation for Dijkstra:
- Priority Queue: Unlike Bellman-Ford, which relaxes all edges V-1 times, Dijkstra’s algorithm uses a priority queue to ensure that the vertex with the smallest known distance is processed first. This reduces the number of unnecessary relaxations.
- Greedy Choice: Dijkstra’s algorithm always picks the “greedy” choice (the closest unvisited vertex) to relax edges, ensuring that each vertex is processed in the correct order.
Note: Handling of Negative Cycles
- 1st version:
- With visited Array:
- The implementation will not enter an infinite loop because once a node is marked as visited, it won’t be reprocessed even if there’s a shorter path found later due to a negative cycle. However, the result will be incorrect because Dijkstra’s algorithm assumes non-negative weights, and negative cycles can lead to incorrect shortest path calculations.
- Will not enter an infinite loop but will produce incorrect results when negative cycles are present.
- With visited Array:
- 2nd Version:
- Without visited Array:
- My implementation could indeed fall into an infinite loop if there are negative cycles. Since the visited array isn’t used, the algorithm would keep finding “shorter” paths due to the negative cycle and continue adding the same nodes back to the priority queue, leading to an infinite loop. This is because, without a visited array, the algorithm continuously tries to improve the shortest path, which is not possible to do correctly in the presence of negative cycles.
- Without the visited array, it can indeed enter an infinite loop in the presence of negative cycles because it will continuously attempt to reduce the path cost in such cycles.
- Without visited Array:
Why Dijkstra’s Algorithm Isn’t Suitable for Graphs with Negative Cycles ?
Dijkstra’s algorithm inherently assumes that all edge weights are non-negative. It is not designed to handle negative weights, let alone negative cycles, because the algorithm’s greedy approach relies on the premise that once the shortest path to a node is found, it cannot be improved. Negative cycles break this assumption, leading to incorrect results or infinite loops.
When not to use Dijkstra's algorithm?
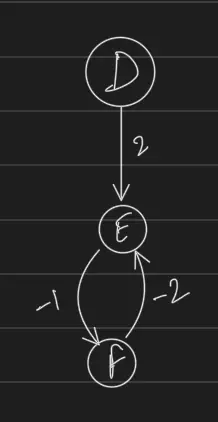
- Negative cycle: Can cause infinite loops as the algorithm continually finds “better” paths by circling the negative cycle.
- The algorithm enters an infinite loop, continuously reducing the path cost by circling the negative cycle E → F → E. It will never terminate because it keeps finding “better” paths with lower total weights.
- Negative edge weights: Dijkstra’s greedy approach assumes adding an edge never decreases path length, which negative edges violate. In such cases, you should use algorithms like Bellman Ford or Floyd Warshall algorithm. (Refer, the above diagram)
- The algorithm fails because it greedily chooses the direct path to C and marks it as final, never considering that a seemingly longer initial path (through B) could lead to a shorter overall path due to the negative edge.
- When you need to find all shortest paths, not just one: If you need to find the shortest paths between all pairs of vertices in the graph, Dijkstra’s algorithm is not the most efficient choice. Floyd-Warshall algorithm would be more suitable for all-pairs shortest paths.
- Dense graphs: For dense graphs, where the number of edges is close to the square of the number of vertices, Dijkstra’s algorithm may not be the most efficient. In such cases, algorithms like Floyd-Warshall algorithm might perform better. Edge weights change dynamically : Dijkstra assumes static edge weights; changing weights can invalidate previously computed paths.
- Unweighted graphs: BFS is enough.